絞り開けるとボケる

一番わかりやすいのが「絞りの値を小さくする」ことでボケが大きくなります。

単焦点レンズなどがボカしやすいのは、開放F値が低いことにあります。

左 (上) から f/2.8 、f/2.0 、f/1.6 (f/1.4で撮るつもりが間違えました(^^;) で撮影しています

望遠を使うとボケる

次も感覚的に理解されやすい「望遠レンズを使う」ことでボケやすくなります。

広角レンズでは絞りを開いても余りボケが大きくならない傾向にあり、望遠レンズでは絞り値が大きくてもボケボケの画が撮りやすい傾向にあります。

但し、これには条件があり「背景が十分に離れている場合」に限ります。

※屋内だと比較写真が撮れないので出かけた際に撮影して更新します

被写体に近付くとボケる

この辺りから意識していない方が増えてくるのではないでしょうか？
「被写体に近付く」こともボケを得やすい条件の一つです。

マクロ撮影などをしたことがある方は分かりやすいと思いますが、被写体に近付くとかなり絞ってあげないと十分な被写界深度が得られない場合が良くあります。
逆に遠景では開放で撮影しても全体にピントが合いやすいです。
(夜に遠くの夜景を手持ちで撮る場合などは開放で撮ればシャッター速度が稼げます)

(左)被写体に近付くとf/8.0ですが、かなりボケます。(右)逆に被写体が遠景だとf/1.6でも殆どボケません。

背景が被写体から離れるとボケる

最後は被写体と背景の距離です。
「被写体と背景の距離をとる」ことで背景をボカしやすい状態にできます。

ボケはピント面から外れるほど大きくなるのは感覚的にも分かると思います。

先の被写体に近付くのも、カメラから被写体までの距離と被写体から背景までの距離を “相対的に” 大きくすることと捉えることもできますね。

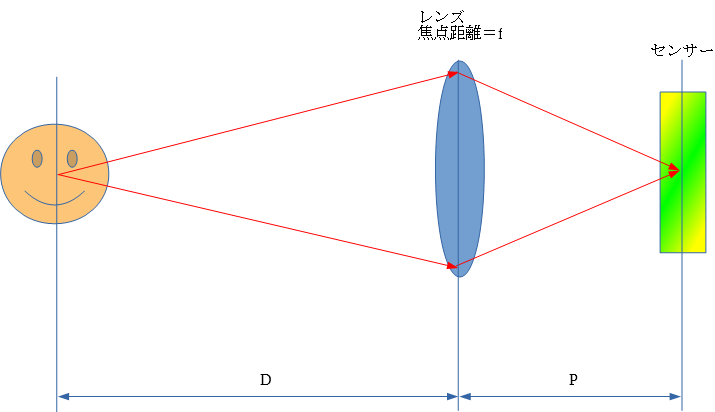
レンズの法則 1/f=1/D+1/P

レンズは以下の式を満足するように作られた光学部品です。

$$
\frac{1}{f}=\frac{1}{D}+\frac{1}{P}
~~~
-(式1)
~~~
\begin{cases}
f : レンズの焦点距離 \\
D : レンズから被写体までの距離 \\
P : レンズからセンサーまでの距離
\end{cases}
$$

レンズの位置は、ピントを合わせる際に移動します。
これによりDとPを調整して被写体をセンサー上に結像させます。

被写体と背景・前景の違い

通常は被写体にピントを合わせますよね。
すると、上で記載した数式に従ってレンズの位置が決まります。
(fと(D+P)が決まっている為)

レンズ位置に対してピント面はある1面だけになるので、背景・前景はセンサー面でない位置で結像することになります。

この時にセンサー面でない位置で結像した光は直進し続けるのでセンサーに届く光は拡散されて届くことになります。前景の場合は、結像するまでの集光途中でセンサーに届きます。
点光源が拡散される大きさがいわゆる “錯乱円” です。
お察しの通り、錯乱円Cが大きければ大きいほど、良くボケます。

ボケ量の理論式を導出しよう！

ではボケ量の理論式を上記の法則から導出します。
ボケは点光源として考えれば十分なので点光源がどれだけの大きさに見えるかで判定します。

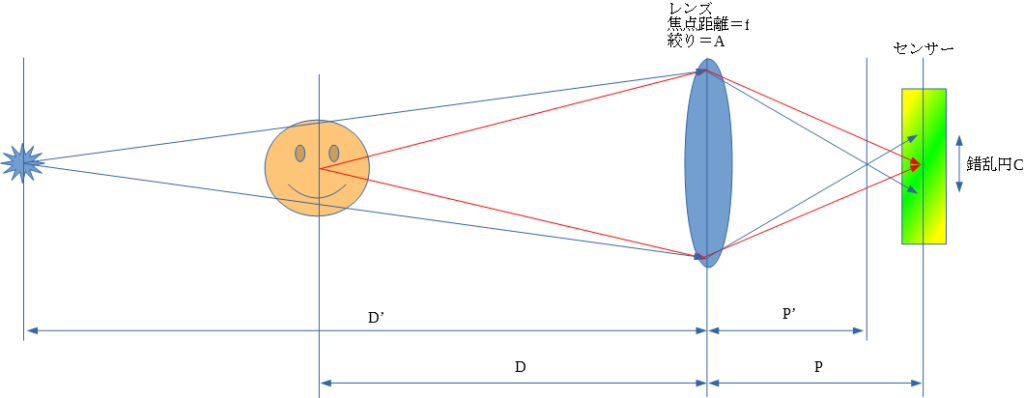
被写体までの距離をD、点光源までの距離をD’として被写体にピントが合った状態でのセンサーまでの距離をそれぞれP、P’とおきます。
また、絞りはAとしておきましょう。

ここで、レンズの絞りは、有効口径比とも呼び光を取り込める口径 (絞り羽で遮られていない光の通り道) と焦点距離の比で表されます。
f/1.0なら焦点距離と同じ直径の口径であるということです。
f/2.0ならf/1.0の半分です。直径なので絞りを倍にすると光量が1/4になります。

先ほどの式1を変形するとレンズからセンサーまでの距離Pは、以下になります。

$$
P=\left(\frac{1}{f}-\frac{1}{D}\right)^{-1}
~~~
-(式2)
$$

点光源が結像する位置P’についても同様に求められます。

しかし、点光源の結像位置P’はセンサー面にありません。
従って、結像位置からセンサーまでのズレた分だけボケます。

この時のボケ量 (錯乱円の直径C) は、絞りによる有効口径と、P’と点光源の結像位置からセンサーまでの距離(P-P’)の比、の積で求まることが先ほどの図から分かります。

$$
C=\frac{f}{A}\cdot\frac{P-P’}{P’}
~~~
-(式3)
$$

式3を式2を使って、被写体までの距離に書き換えます。

$$
C=\frac{f}{A}\cdot\frac{(D’-D)f}{(D-f)D’}
~~~
-(式4)
$$

レンズからセンサーまでの距離は被写体までの距離に比べると小さいことが多い (マクロ撮影以外) ので、DやD’はカメラから被写体までの距離と考えてOKです。
厳密にマクロ撮影まで考えるなら式2を加えて考えます。

式4だとどうすればボケが大きくなるのか分かりにくいので、右側の分数の分母・分子をD’fでそれぞれ割って整理します。

$$
C=\frac{f}{A}\cdot\frac{1-\frac{D}{D’}}{\frac{D}{f}-1}
~~~
-(式4′)
$$ $$
※式1よりピントが合っている状態ではD>fです
$$

式4’を見れば一般的に言われているボケを大きくする方法と合致します。
これでボケ量の定量的な評価ができます。

• 絞りを開ける → Aが小さくなるのでCが大きくなる
• 望遠を使う → fが大きくなるのでCが大きくなる
• 被写体に近付く → Dが小さくなるのでCが大きくなる
• 背景を遠ざける → D’が大きくなるのでCが大きくなる

ボケ量を実際に計算してみましょう！

では、ボケ量がどのように変化するのか計算してみます。

錯乱円の直径だとどの程度のボケ感か分かりにくいので、センサーサイズの縦寸法に対する比率に変換します。
(アスペクト比3:2の2400万画素だと0.025%が1画素に相当します)
・フルサイズ ： 35.9×24.0mm
・APS-C　　 ： 23.5×15.6mm

被写体を5mの位置とした時のボケ量を計算してグラフにすると以下のようになります。

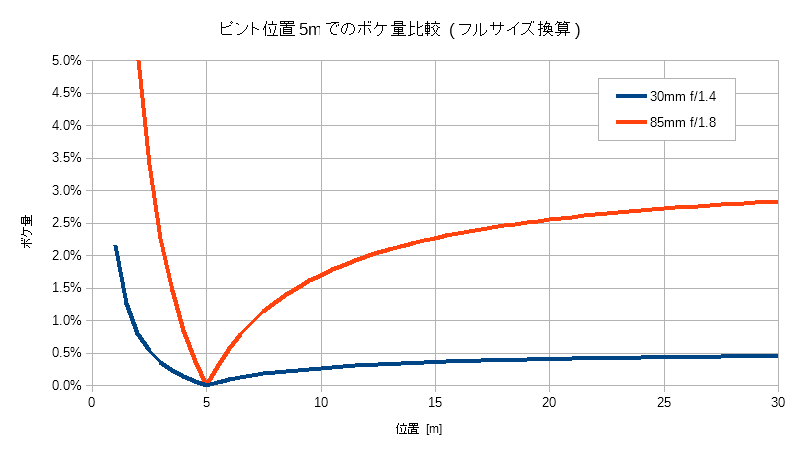
数値計算例も以下に記載するのでご確認下さい。
以下は Javascript による自動計算です。